LA PUISSANCE DE LA GÉOSTATISTIQUE POUR CARTOGRAPHIER LE NIVEAU D'UNE NAPPE À L'ÉCHELLE RÉGIONALE - MESURES PIÉZOMÉTRIQUES EN CALIFORNIE
Le réseau régional piézométrique collecte périodiquement le niveau de la nappe en Californie, sur une zone surveillée de
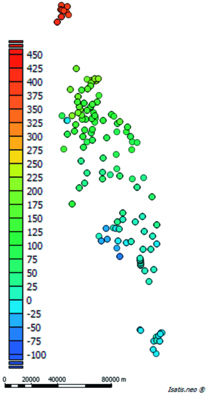
300 km de longueur et 70 km de largeur. Les données acquises sont disponibles publiquement en deux formats, journalier et mensuel (1). Un extrait des données disponibles est choisi dans le but de cartographier le niveau de la nappe.
Cet extrait contient les moyennes du niveau de la nappe au mois de mai 2021 dans 160 piézomètres.
MÉTHODES GÉOSTATISTIQUES POUR CARTOGRAPHIER
Les méthodes géostatistiques sont utilisées pour cartographier (en 2D) ou modéliser (en 3D) des
données géoréférencées avec des coordonnées cartésiennes issues d’échantillons géologiques,
chimiques, radiologiques ou de mesures géotechniques, géophysiques ou, comme ici, hydrogéologiques.
Dans cette application, deux méthodes géostatistiques sont comparées afin de cartographier
le niveau de la nappe à l’échelle régionale. Néanmoins, les méthodes présentées peuvent
aussi être appliquées sur des données hydrogéologiques à d’autres échelles.
À courte distance, les mesures hydrogéologiques sont normalement ressemblantes. À plus
grande distance, ces mesures montrent souvent une dérive liée aux situations géomorphologiques
ainsi que météorologiques.
Cette ambivalence naturelle doit être considérée dans la modélisation afin de produire une carte qui reflète non seulement la dérive régionale, mais aussi le comportement du niveau de la nappe à courte distance où les mesures sont disponibles.
À cet égard, les méthodes géostatistiques utilisées sont le krigeage ordinaire et le krigeage universel. Les deux méthodes en question permettent dans un certain nombre de cas de cartographier
les phénomènes non stationnaires (avec une dérive ou une variation de la moyenne dans l’espace). La méthode de krigeage ordinaire est la plus fréquemment utilisée par les géostatisticiens.
La méthode de krigeage universel transforme les mesures non stationnaires en données résiduelles stationnaires par la soustraction d’une dérive globale inférée entre le niveau de la nappe et les coordonnées des mesures. La dérive inférée dans cette étude est un modèle polynomial de degré deux (une parabole) ajusté entre la coordonnée Y et le niveau de la nappe. Dans la littérature, d’autres modèles expérimentaux ou numériques sont proposés pour les cas particuliers, notamment en présence de pompage ou d’injection(2-4).
ANALYSE DE STATIONNARITÉ : Y A-T-IL UNE DÉRIVE ?
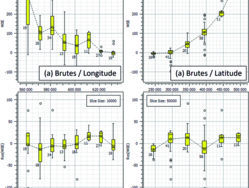
Dans un projet de cartographie, l’analyse de stationnarité est une étape fondamentale qui permet de mieux connaître les données d’entrée ainsi que de choisir une méthode d’interpolation adaptée. À cet égard, la distribution statistique de la variable à l’étude, ici le niveau de la nappe, est comparée dans les différentes sections longitudinales et latitudinales et présentée par les boîtes à moustaches sur l’illustration 2a. Le long de la latitude, une dérive au deuxième degré est évidente, c’est-à-dire l’augmentation du niveau de la nappe en direction du nord. Le long de la longitude, une diminution du
niveau de la nappe est observée.
Néanmoins cette courbe est biaisée par la configuration spatiale des données en direction NNW (cf. illustration 1) car les données acquises à l’ouest ont des latitudes plus élevées.
Par conséquent, le modèle de la dérive spatiale est développé entre la latitude et le niveau de la nappe (Eq. 1), puis les résiduelles sont calculées par la soustraction du niveau de la nappe
(Water Surface Elevation ou WSE) (Eq. 2). L’analyse de stationnarité sur les données résiduelles confirme qu’il n’existe plus de dérive longitudinalement et latitudinalement (iIllustration 2b), et que la
moyenne et la variance du niveau de la nappe sont stationnaires dans les deux directions.
Der = 190 891 - 0,08917 × Y + 1.041 ×10-8 × Y2 Eq. 1
Res = WSE - Der Eq. 2
ANALYSE VARIOGRAPHIQUE : QUEL COMPORTEMENT SPATIAL ?
La cartographie géostatistique tient compte de la variabilité spatiale du phénomène modélisé lors de l’analyse variographique. Le modèle du variogramme ajusté sur les points expérimentaux détermine :
i) la distance maximale de la corrélation spatiale qui aide à définir la distance maximale du voisinage pour interpoler chaque point cible (grille d’interpolation) ;
ii) les poids affectés aux données dans le voisinage de chaque cible pour l’interpolation.
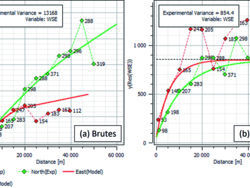
L’analyse variographique est réalisée sur les données brutes (illustration 3a). Elle confirme une variabilité plus importante latitudinalement, avec des paliers différents, correspondant à une anisotropie zonale. De plus, le variogramme le long de la latitude est sans borne (palier), autre diagnostic de non-stationnarité observée sur l’illustration 2a. Le modèle ajusté sur l’illustration 3a est valide pour les distances inférieures à 40 km ; au-delà, le modèle est extrapolé.
Afin d’exclure les valeurs du variogramme non connues, une limite de voisinage peut être considérée dans un rayon de 20 à 25 km de la cible d’interpolation.
La distance entre les données dans le voisinage ne dépasse alors pas le diamètre du voisinage, ce qui assure l’exclusion des distances au-delà de la distance d’extrapolation du variogramme, c’est-à-dire environ 40 km.
Quant aux variogrammes sur les résiduelles (illustration 3b), ils montrent un palier et plus d’anisotropie zonale. Cependant, une anisotropie géométrique est constatée, avec une portée plus importante le long de la latitude.
Les données résiduelles étant stationnaires, il n’est plus nécessaire d’imposer une limite du voisinage. Les paramètres des modèles de variogramme ajustés sont décrits dans les Eq. 3 et 4.
YB(h) = Nug(00) + Sph(1000,
[40 km, 20 km]) + Sph(12000,
[300 km,1000 km]) Eq. 3
YR(h) = Nug(50) +Sph(800,
[35 km,18 km]) Eq. 4
SYNTHÈSE
La géostatistique est un ensemble de techniques reposant sur une théorie éprouvée, permettant d’analyser et modéliser des données spatiales.
L’analyse géostatistique d’une variable non stationnaire est plus complexe en raison d’une variabilité spatiale plus importante du phénomène à l’étude.
Pour modéliser un phénomène non stationnaire, il existe deux approches : diviser l’espace en sous-unités plus homogènes ou transformer la variable non stationnaire en une variable stationnaire.
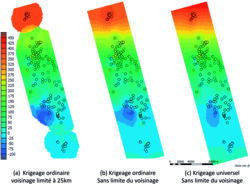
Dans cet article, la deuxième approche est utilisée en appliquant la méthode du krigeage universel. Après avoir comparé avec le krigeage ordinaire, la carte obtenue par krigeage universel montre une
erreur absolue inférieure. Visuellement, la carte obtenue par krigeage universel montre moins d’artefacts et permet une extrapolation dans les zones avec moins d’information. Tous les calculs géostatistiques, les cartes et les graphiques sont réalisés avec le logiciel Isatis.neo, développé par Geovariances.
Pedram Masoudi, Hélène Binet et Claire Faucheux
Geovariances
Bibliographie
1. California Department of Water Resources, 2023, Periodic Groundwater Level Measurements,
https://data.cnra.ca.gov/dataset/periodic-groundwater-level-measurements, accessed 11/28/2023.
2. M. J. Tonkin and S. P. Larson, “Kriging Water Levels with a Regional-Linear and Point-Logarithmic
Drift,” Groundwater, vol. 40, no. 2, pp. 185–193, Mar. 2002.
3. M. Karanovic, M. Tonkin, and D. Wilson, “KT3DH2O : A program for kriging water level data using
hydrologic drift terms,” Ground Water, vol. 47, no. 4, pp. 580–586,2009.
4. S.S.Papadopulos&Associates.Inc., KT3D_H2O Version 3.0 - A Program for Kriging Water
Level Data using Hydrologic Drift Terms. S. S. Papadopulos & Associates, Inc.